|
Abstract
Given a p-dimensional proximity matrix
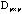 , a sequence* of correlation matrices, , a sequence* of correlation matrices,
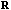 =( =(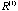 , ,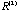 ,…), is iteratively formed from it. Here ,…), is iteratively formed from it. Here
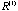 is the correlation matrix of the original proximity matrix D and is the correlation matrix of the original proximity matrix D and
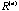 is the correlation matrix of is the correlation matrix of
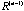 , n > 1. The sequence R often converges to a matrix , n > 1. The sequence R often converges to a matrix
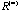 whose elements are +1 or -1. This special pattern of whose elements are +1 or -1. This special pattern of
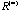 partitions the p objects into two disjoint groups and it can be recursively applied to generate a divisive hierarchical clustering tree. While convergence is itself useful, we are even more concerned with what happens before convergence. We discover that before convergence, there is a rank reduction property with elliptical structure. When rank of partitions the p objects into two disjoint groups and it can be recursively applied to generate a divisive hierarchical clustering tree. While convergence is itself useful, we are even more concerned with what happens before convergence. We discover that before convergence, there is a rank reduction property with elliptical structure. When rank of
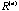 reaches two, the column vectors on reaches two, the column vectors on
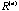 fall on an ellipse on a two-dimensional subspace. This unique order of relative positions for the p points on the ellipse can be used to solve seriation problems such as the reordering of a Robinson matrix. A software package, Generalized Association Plots (GAP), is developed which utilizes modern computer's graphic ability to retrieve important information hidden in the data or proximity matrices. fall on an ellipse on a two-dimensional subspace. This unique order of relative positions for the p points on the ellipse can be used to solve seriation problems such as the reordering of a Robinson matrix. A software package, Generalized Association Plots (GAP), is developed which utilizes modern computer's graphic ability to retrieve important information hidden in the data or proximity matrices.
KEY WORDS: Data visualization, Divisive clustering tree, Latent structure; Perfect symmetry; Proximity matrices,
Seriation.
* This correlation sequence was first introduced by McQuitty (1968).
Breiger, Boorman & Arabie (1975) also developed an algorithm, CONCOR, based on their rediscovery of the convergence of this sequence.
Reference:
-
Breiger, R. L.,
Boorman, S. A. and Arabie, P (1975), "An Algorithm for Clustering Relational Data with Applications to Social Network Analysis and Comparison with Multidimensional Scaling," Journal of Mathematical Psychology, 12, 328-383.
-
McQuitty, L. L. (1968), "Multiple Clusters, Types, and Dimensions from Iterative Intercolumnar Correlational Analysis," Multivariate Behavioral Research, 3, 465-477.
|