|
3 the convergence problem
Instead of using an existing seriation algorithm to find the permutation needed to reshape the proximity matrix in order to extract the embedded structure, we take a different approach. Given a proximity matrix D, a sequence of sample Pearson product moment correlation matrices is iteratively formed from D,
 =( =( , ,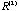 ,…), where ,…), where
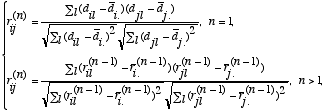
and
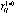 and and 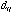 are the ijth entry of
are the ijth entry of 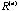 and D, respectively. Under certain circumstance, this sequence of correlation matrices converges to a matrix and D, respectively. Under certain circumstance, this sequence of correlation matrices converges to a matrix
 . We study the convergence behavior of the sequence and the structure in . We study the convergence behavior of the sequence and the structure in
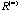 , and apply this to give new seriation methods for the reconstruction of D. This section describes the convergence and the following sections give a detailed discussion of the structure found and its
application. , and apply this to give new seriation methods for the reconstruction of D. This section describes the convergence and the following sections give a detailed discussion of the structure found and its
application.
To see some of this, Figure 3 shows the colored maps (a sorted version of Figure 3 is given in Section 5.5 as Figure 11) of the sequence of correlation matrices for our fifty symptoms example. In fact it takes twelve iterations for this sequence of correlation matrices to converge to the limiting matrix
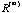 which has all elements equal to plus one or minus one. which has all elements equal to plus one or minus one.
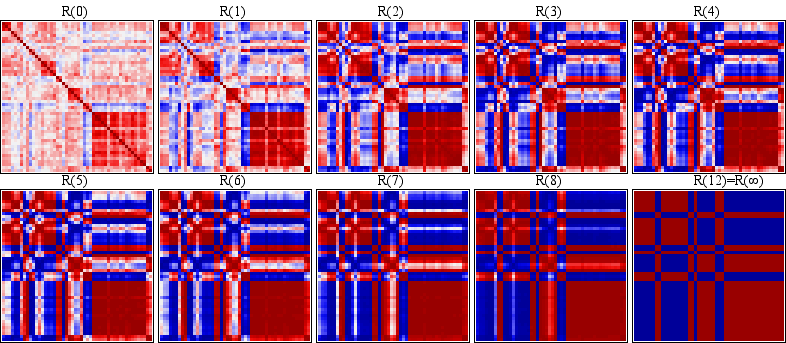
Figure 3. Maps for the Converging Sequence of Correlation Matrices for the Fifty Symptoms.
From the sequence of sorted colored maps in Figure 11, note that the groups of variables with high correlation coefficients formed at earlier iterations behave like gravity centers. At each iteration these groups compete with each other and attract the ungrouped variables and the smaller groups to form larger and stronger (more coherent) groups. The between-group structure also becomes more and more distinct. Finally, only two centers survive in the converged status
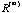 (plus and minus ones). (plus and minus ones).
The convergent sequence of the iteratively formed correlation matrices has several distinctive properties. This section illustrates these properties and the applications are given in next few sections.
|