|
3.2 Will the Sequence Converge?
The iteratively formed correlation matrices for the fifty symptom example does converge to the limiting matrix
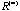 with positive and negative ones. But does the sequence of iteratively formed sample Pearson correlation matrices always converge? If so, does it always converge to a limiting matrix with positive and negative ones. But does the sequence of iteratively formed sample Pearson correlation matrices always converge? If so, does it always converge to a limiting matrix
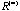 with only positive and negative ones? The first answer seems to be Yes because this is so according to the computer output for all examples we have studied including an extensive computer simulation generating numerous sample correlation matrices with various dimension and correlation structure. Unfortunately, we cannot prove it yet. What we have known at this moment are some weaker statements. with only positive and negative ones? The first answer seems to be Yes because this is so according to the computer output for all examples we have studied including an extensive computer simulation generating numerous sample correlation matrices with various dimension and correlation structure. Unfortunately, we cannot prove it yet. What we have known at this moment are some weaker statements.
It is easy to verify that the mapping
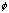 defined in the beginning of Section 1 is continuous at any correlation coefficient matrix R except for the special case where R is degenerate. A correlation matrix R is called non-degenerate if all its diagonal entries are one and no column of R equals 1, where 1=(1,…,1)T, and is called degenerate if otherwise. Since the set of all correlation matrices is compact and the mapping is differentiable , it can be speculated that some fixed point theorems can be used to prove the convergence. But this is not quite so trivial due to the existence of chaotic mapping. defined in the beginning of Section 1 is continuous at any correlation coefficient matrix R except for the special case where R is degenerate. A correlation matrix R is called non-degenerate if all its diagonal entries are one and no column of R equals 1, where 1=(1,…,1)T, and is called degenerate if otherwise. Since the set of all correlation matrices is compact and the mapping is differentiable , it can be speculated that some fixed point theorems can be used to prove the convergence. But this is not quite so trivial due to the existence of chaotic mapping.
In an unpublished article, Kruskal (1977) attempts to prove convergence with partial success. He needs conditions over
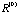 , which are complicated. A related question to convergence is to find the stationary points R for , which are complicated. A related question to convergence is to find the stationary points R for
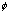 : : 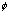 (R)=R. It is easy to see that if R consists of +1 or -1, then R is a stationary point. Are they the only ones? The answer is no. Figure 5 in Section 4.2 gives all stationary points for p=3, and 4. (R)=R. It is easy to see that if R consists of +1 or -1, then R is a stationary point. Are they the only ones? The answer is no. Figure 5 in Section 4.2 gives all stationary points for p=3, and 4.
3.3 The Decreasing Sequence of Ranks
While convergence is important in itself, we are even more concerned about what happens before convergence. What we found is an interesting rank reduction property with elliptical structure which we shall explore for seriation and clustering later. At each iteration, groups become more coherent while each individual column gradually loses its identity. The high dimensional structure collapses to a lower dimensional structure each time two or more columns move close enough to their common corner. We have the following observation.
Lemma 3.5.
The ranks of {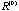 , ,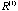 , ,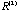 ,…}, { ,…}, { , ,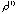 , ,
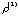 ,…}, form a nonincreasing sequence. ,…}, form a nonincreasing sequence.
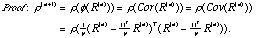
Since 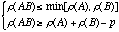 (Sylvester's Law of Nullity), we have
(Sylvester's Law of Nullity), we have
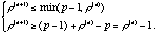 This completes the proof.
This completes the proof.
Two facts also emerge from the proof: if the original correlation matrix
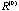 is of full rank ( is of full rank (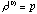 ), the rank of ), the rank of
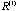 will be reduced by 1 ( will be reduced by 1 (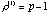 ); the rank can only be reduced by at most 1 at each iteration. ); the rank can only be reduced by at most 1 at each iteration.
For our numerical results, the rank is calculated as the number of eigenvalues greater than
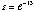 . Different sizes of . Different sizes of  could result in slightly different rank lists. For our case study in Figure 1, it takes twelve iterations for the sequence to converge to
could result in slightly different rank lists. For our case study in Figure 1, it takes twelve iterations for the sequence to converge to
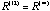 . The ranks are {50, 49, 49, 40, 20, 7, 3, 2, 2, 2, 2, 2, 1}. Theoretically this can't occur since the reduction of rank can't exceed one at each iteration. Only the first iteration is guaranteed to reduce the rank by one. It is possible that all the ranks for the rest of the matrices in the sequence equal 49 theoretically. But the structure of the column space spanned by . The ranks are {50, 49, 49, 40, 20, 7, 3, 2, 2, 2, 2, 2, 1}. Theoretically this can't occur since the reduction of rank can't exceed one at each iteration. Only the first iteration is guaranteed to reduce the rank by one. It is possible that all the ranks for the rest of the matrices in the sequence equal 49 theoretically. But the structure of the column space spanned by
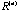 becomes flatter and flatter and eventually collapses to a lower dimensional structure. becomes flatter and flatter and eventually collapses to a lower dimensional structure.
Besides, while the numerical rank decreases from p to 1, the sum of squares of the
eigenvalues, which is equal to the sum of squares of all 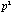 elements in the correlation matrix, increases to
elements in the correlation matrix, increases to 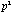 at
at 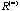 . That is, the variation becomes more and more concentrated on the leading eigenvectors. For example, the sum of squares of the eigenvalues for the sequence of matrices are (237.0, 514.6, 933.7, 1214.4, 1313.0, 1383.1, 1517.7, 1761.0, 2119.1, 2436.5, 2499.1, 2500.0, 2500.0) (Figure 8b). However, this increasing trend may not be true at early iterations for a highly homogeneous proximity matrix D. . That is, the variation becomes more and more concentrated on the leading eigenvectors. For example, the sum of squares of the eigenvalues for the sequence of matrices are (237.0, 514.6, 933.7, 1214.4, 1313.0, 1383.1, 1517.7, 1761.0, 2119.1, 2436.5, 2499.1, 2500.0, 2500.0) (Figure 8b). However, this increasing trend may not be true at early iterations for a highly homogeneous proximity matrix D.
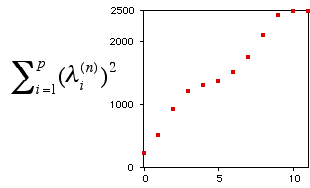
Figure 8 (b). Plot of the Sequence of Summations of Squared Eigenvalues for each Iteration for the Fifty Symptoms.
Reference:
|