|
4.2 The Symmetrical Converging structure
The general form of
 in the case of symmetry is in the case of symmetry is
 . .
It need not be that all
 pairs of measurement are identical, but there still exists structures wherein the p points can't be divided into two groups. Figure 7 summarizes all the possible symmetry and non-symmetry structures with their corresponding limits for p=3 and p=4. The number of possible limits is an increasing function of p. pairs of measurement are identical, but there still exists structures wherein the p points can't be divided into two groups. Figure 7 summarizes all the possible symmetry and non-symmetry structures with their corresponding limits for p=3 and p=4. The number of possible limits is an increasing function of p.
In general there are only three types of columns in a converged pattern matrix:
-
columns with only plus and minus ones in a rank-1 matrix, patterns 3(3), 4(5), and 4(6) for example;
-
columns with summation of elements equal to zero. (this type of matrix can be further divided into two subtypes- one for symmetry, patterns 3(1) and 4(1) for instance; the other for a circular matrix, patterns 3(1), 4(2) and part of 4(3));
-
columns for symmetry
center(s) with zeroes to all other points, column B in pattern 3(2), column D in pattern 4(3), and columns B/C in pattern 4(4) for example. Section 5.4 studies the possible applications of using the symmetry patterns to study the crystallographic structure.
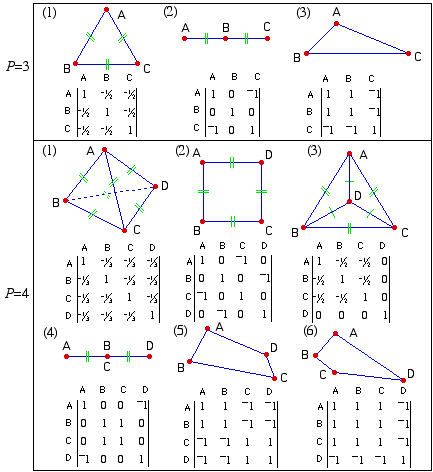
Figure 7. All possible Symmetry and Non-Symmetry Structures with the
Corresponding Converged Pattern Matrices for p=3 and 4.
We usually do not encounter proximity matrices with a perfect symmetric structure in a medical study of the sort looked at here. One can search for a proximity matrix with a symmetric structure in physics, chemistry or molecular biology.
|