|
4 The General Converging Patterns
With different types of structure embedded in the proximity matrix D, there are many possible types of converged matrix
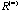 and two that are major: non-symmetry and symmetry. and two that are major: non-symmetry and symmetry.
4.1 The Rank-One non-symmetry converged matrix
For practical statistical data analyses only one special type of converging matrix
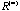 can occur. That is the rank-one correlation matrix with all elements equal to plus or minus one. Here the ellipsoid has dimension one and all the p vectors fall on the two points on the vertices. The grouping effect of the positive and negative ones can be used to split the p variables (objects) into two groups. can occur. That is the rank-one correlation matrix with all elements equal to plus or minus one. Here the ellipsoid has dimension one and all the p vectors fall on the two points on the vertices. The grouping effect of the positive and negative ones can be used to split the p variables (objects) into two groups.
Starting with a proximity matrix, the associated sequence of correlation matrices usually converges in about ten iterations. The p objects are automatically divided into two groups according to
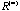 . Such partition has some nice simulation results with the following splitting criterion, . Such partition has some nice simulation results with the following splitting criterion,
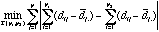 , ,
where  stands for all possible splitting of p objects into groups of
stands for all possible splitting of p objects into groups of 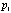 and
and  . .
Example 4.1 500 sets of 20 bivariate uniform (0,1) observations are generated. For each set, all the
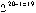 =524,288 possible partitions are compared with the splitting correlation result and the frequencies of the number of partitions that performed better than our method is calculated. The correlation split method finds the best partition among all the 524,288 possible partitions in about 60%(298/500) of the simulations. In more than 90%(456/500) of simulations, our method stands at the 1st to sixth place among all the 524,288 possible combinations. The worst case is a 446-th order, which stands at 99.9149322 percentile. Section 5.3 shows how this splitting rule can be recursively applied to the proximity matrix to grow a divisive hierarchical clustering tree. =524,288 possible partitions are compared with the splitting correlation result and the frequencies of the number of partitions that performed better than our method is calculated. The correlation split method finds the best partition among all the 524,288 possible partitions in about 60%(298/500) of the simulations. In more than 90%(456/500) of simulations, our method stands at the 1st to sixth place among all the 524,288 possible combinations. The worst case is a 446-th order, which stands at 99.9149322 percentile. Section 5.3 shows how this splitting rule can be recursively applied to the proximity matrix to grow a divisive hierarchical clustering tree.
|