|
6 more features of GAP
We have shown that the converging sequence has many powerful and useful properties that can be applied in many areas of multivariate statistical analysis. In this section, We use the psychosis disorder data with 95 patients on 50 symptoms to illustrate the framework of a complete GAP analysis, in Figure 9. GAP integrates the following four major steps to extract and summarize information embedded in a multivariate data set with n subjects and p variables.
6.1 Raw Data and Proximity Matrix Maps with Suitable Color Projection
The raw data matrix is denoted as
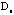 . A gray spectrum is applied to project ordinal numbers into gray dots with different intensities. The correlation matrix is calculated as the proximity matrix . A gray spectrum is applied to project ordinal numbers into gray dots with different intensities. The correlation matrix is calculated as the proximity matrix
 for the 50 symptoms. For the 95 patients, also the correlation matrix is used as the proximity matrix for the 50 symptoms. For the 95 patients, also the correlation matrix is used as the proximity matrix
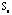 (We also tried the Euclidean (standardized) distance). The diverging blue-red color scheme is used to represent the bi-directional property of the correlation coefficients. For a data profile with various variable scales, the variables can be transformed (standardized) and projected through suitable color spectrum to represent the characteristics of the scales. Covariance matrix with the Euclidean (standardized) distance matrix can also be calculated as (We also tried the Euclidean (standardized) distance). The diverging blue-red color scheme is used to represent the bi-directional property of the correlation coefficients. For a data profile with various variable scales, the variables can be transformed (standardized) and projected through suitable color spectrum to represent the characteristics of the scales. Covariance matrix with the Euclidean (standardized) distance matrix can also be calculated as
 and and 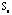 . .
6.2 The Sorted Matrix Maps with the Principle of Geometry
The next step is to form the sequences of correlation matrices for
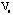 and and 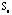 to identify the ellipses
to identify the ellipses 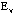 and and  at iteration 7 and 5 respectively. The elliptical seriations for the patients and the symptoms are then applied to arrange the two correlation matrices
at iteration 7 and 5 respectively. The elliptical seriations for the patients and the symptoms are then applied to arrange the two correlation matrices
 and and 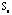 into
into 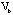 and and 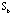 . The same seriations are also used to reshape the raw data matrix . The same seriations are also used to reshape the raw data matrix
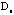 into into 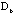 . The difference between . The difference between
 and and  is not much since
is not much since 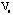 is already grouped by the SAPS and SANS symptom tables. However, there is a dramatic change from is already grouped by the SAPS and SANS symptom tables. However, there is a dramatic change from
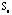 to to 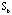 since the patients are admitted in a random order. There is a clear latent structure in
since the patients are admitted in a random order. There is a clear latent structure in
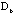 . A band of dark gray dots moves from the upper right corner to the lower left corner. Since the seriations for . A band of dark gray dots moves from the upper right corner to the lower left corner. Since the seriations for
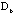 are identical to those for are identical to those for  and
and  , these three maps are closely related to each other and should be cross-examined to find the information embedded in the raw data matrix and two proximity matrices. , these three maps are closely related to each other and should be cross-examined to find the information embedded in the raw data matrix and two proximity matrices.

Figure 9. Complete GAP Procedure for the Psychosis Disorder Data Set with Ninety-five Patients and Fifty Symptoms.
Without a suitable seriation to arrange these matrix-maps such that rows and columns with similar (distinct) properties are placed at closer (farther) positions, these matrix maps are useless. We shall call this concept of placing similar (distinct) objects at positions close to (far away from) each other in a plot for representing the association structure the principle of geometry. In the graphic tools for continuous variables (histogram, line-plot, scatter-plot, etc.) this geometry-principle always hold because the nature of a continuous variable plot is to represent the metric structure of subjects geometrically. In a raw data matrix map or a proximity matrix map, this principle of geometry has to be forced in with appropriate
seriations.
6.3 Partitioned Matrix Maps with near Stationary Iterations
In Section 5.6, Figure 8a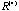 partitions the correlation matrix of the fifty symptoms into five major groups. In this section we take a look at the possible patient-clusters and the general behavior of patient-clusters on symptom-groups. It seems that there is no clear patient-cluster structure in partitions the correlation matrix of the fifty symptoms into five major groups. In this section we take a look at the possible patient-clusters and the general behavior of patient-clusters on symptom-groups. It seems that there is no clear patient-cluster structure in
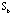 except the negative between-group correlations on the off-diagonal area. It takes nine iterations for except the negative between-group correlations on the off-diagonal area. It takes nine iterations for
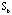 to converge and to split all the 95 patients into two groups. The first group is a mixed group of 26 bipolar-disorder patients with 12 schizophrenia patients and the second is a pure group with 57 schizophrenia patients. to converge and to split all the 95 patients into two groups. The first group is a mixed group of 26 bipolar-disorder patients with 12 schizophrenia patients and the second is a pure group with 57 schizophrenia patients.
In Figure 9c (= (=
 ), a coherent group on the upper left corner with sharp edges is easily identified. This group, to be denoted as S0, comes with all 26 bipolar-disorder patients and only 4 schizophrenia patients. At the lower right corner, there is a large group, S1, of pure schizophrenia patients but the structure is not as tight as that of S0. In between S1 and S0 is a group of pure schizophrenia patients but the between group relationship for this group with S1 and S0 are about equal. We shall use S01 to denote this group of patients. ), a coherent group on the upper left corner with sharp edges is easily identified. This group, to be denoted as S0, comes with all 26 bipolar-disorder patients and only 4 schizophrenia patients. At the lower right corner, there is a large group, S1, of pure schizophrenia patients but the structure is not as tight as that of S0. In between S1 and S0 is a group of pure schizophrenia patients but the between group relationship for this group with S1 and S0 are about equal. We shall use S01 to denote this group of patients.
We then plot again the two-way sorted raw data map with the sorted correlation maps for patients at
 and for symptoms at and for symptoms at 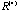 attach to it, in Figure 9c. The green lines represent the partitions for symptom groups and for patient-clusters. The general behavior of patient-clusters on the symptom-groups can be easily identified in
attach to it, in Figure 9c. The green lines represent the partitions for symptom groups and for patient-clusters. The general behavior of patient-clusters on the symptom-groups can be easily identified in
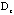 . .
6.4 The Sufficient Graph with Three Multivariate Linkages
In order to extract and summarize the visualized information in Figure 9b, we can further convert these matrix maps into a simplified version. Illustrated in Figure 9d are the mean-structure maps of the three matrices for raw data and proximities. Original proximity matrices for variables and subjects are represented by squares with different mean intensities on the diagonal for within-group structure and rectangles off diagonal for between-group relationship. The double sorted raw data matrix map is also represented by rectangles with various mean-gray intensities to express the interaction effect between each subject-cluster on every variable-group. These three mosaic-displays in Figure 9d contain the principal structural information embedded in the original data set. The mean function in Figure 9d can be replaced with any statistic for displaying desired information structure. We shall name these three mosaic displays the sufficient graph for a multivariate data set. The sufficient graph is then used to answer the three multivariate problems raised by the psychiatrist. Fifty symptoms are divided into five symptom-groups with different within and between group structure. Ninety-five patients are also grouped into three clusters. The general behavior of these three patient-clusters on each of the five symptom-groups can now be easily comprehended. One can always go back to consult the three original sorted matrix maps (Figure 9b) for fear of losing too much information.
|